Mathematics Curriculum Intent
Throughout Westgate Academy’s mathematics curriculum, we aspire for all children to leave with a solid foundation of mathematical knowledge. As stated by the DfE, mathematics is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. We strive for children to become fluent in the fundamentals of mathematics, to reason mathematically, and apply their knowledge to solve complex problems. To understand the connectivity of mathematics and the significance of times tables as a life skill are key foci for us as a school. We want children to develop a love of maths and a curiosity about the subject. We will follow the National Curriculum in a way which meets the needs of each cohort and our individual children.
Curriculum Content Coverage: Year 1 and 2
|
YEAR GROUP
|
Year 1
|
Year 2
|
|
Number and Place Value
|
Pupils should be taught to:
- count to and across 100, forwards and backwards, beginning with 0 or 1, or from any given number
- count, read and write numbers to 100 in numerals; count in multiples of twos, fives and tens
- given a number, identify one more and one less
- identify and represent numbers using objects and pictorial representations including the number line, and use the language of: equal to, more than, less than (fewer), most, least
- read and write numbers from 1 to 20 in numerals and words.
|
Pupils should be taught to:
- count in steps of 2, 3, and 5 from 0, and in tens from any number, forward and backward
- recognise the place value of each digit in a two-digit number (tens, ones)
- identify, represent and estimate numbers using different representations, including the number line
- compare and order numbers from 0 up to 100; use <, > and = signs
- read and write numbers to at least 100 in numerals and in words
- use place value and number facts to solve problems.
|
|
Addition and Subtraction
|
Pupils should be taught to:
- read, write and interpret mathematical statements involving addition (+), subtraction (–) and equals (=) signs
- represent and use number bonds and related subtraction facts within 20
- add and subtract one-digit and two-digit numbers to 20, including zero
- solve one-step problems that involve addition and subtraction, using concrete objects and pictorial representations, and missing number problems such as 7 = – 9.
|
Pupils should be taught to:
- solve problems with addition and subtraction:
- using concrete objects and pictorial representations, including those involving numbers, quantities and measures
- applying their increasing knowledge of mental and written methods
- recall and use addition and subtraction facts to 20 fluently, and derive and use related facts up to 100
- add and subtract numbers using concrete objects, pictorial representations, and mentally, including:
- a two-digit number and ones
- a two-digit number and tens
- two two-digit numbers
- adding three one-digit numbers
- show that addition of two numbers can be done in any order (commutative) and subtraction of one number from another cannot
- recognise and use the inverse relationship between addition and subtraction and use this to check calculations and solve missing number problems.
|
|
Multiplication and Division
|
Pupils should be taught to:
- solve one-step problems involving multiplication and division, by calculating the answer using concrete objects, pictorial representations and arrays with the support of the teacher.
|
Pupils should be taught to:
- recall and use multiplication and division facts for the 2, 5 and 10 multiplication tables, including recognising odd and even numbers
- calculate mathematical statements for multiplication and division within the multiplication tables and write them using the multiplication (×), division (÷) and equals (=) signs
- show that multiplication of two numbers can be done in any order (commutative) and division of one number by another cannot
- solve problems involving multiplication and division, using materials, arrays, repeated addition, mental methods, and multiplication and division facts, including problems in contexts.
|
|
Fractions (including decimals and percentages)
|
Pupils should be taught to:
- recognise, find and name a half as one of two equal parts of an object, shape or quantity
- recognise, find and name a quarter as one of four equal parts of an object, shape or quantity.
|
Pupils should be taught to:
- recognise, find, name and write fractions 1/3, 1/4, 2/4, 3/4 of a length, shape, set of objects or quantity
- write simple fractions for example, 1/2 of 6 = 3 and recognise the equivalence of 2/4 and 1/2.
|
|
Measurement
|
Pupils should be taught to:
- compare, describe and solve practical problems for:
- lengths and heights [for example, long/short, longer/shorter, tall/short, double/half]
- mass/weight [for example, heavy/light, heavier than, lighter than]
- capacity and volume [for example, full/empty, more than, less than, half, half full, quarter]
- time [for example, quicker, slower, earlier, later]
- measure and begin to record the following:
- lengths and heights
- mass/weight
- capacity and volume
- time (hours, minutes, seconds)
- recognise and know the value of different denominations of coins and notes
- sequence events in chronological order using language [for example, before and after, next, first, today, yesterday, tomorrow, morning, afternoon and evening]
- recognise and use language relating to dates, including days of the week, weeks, months and years
- tell the time to the hour and half past the hour and draw the hands on a clock face to show these times.
|
Pupils should be taught to:
- choose and use appropriate standard units to estimate and measure length/height in any direction (m/cm); mass (kg/g); temperature (°C); capacity (litres/ml) to the nearest appropriate unit, using rulers, scales, thermometers and measuring vessels
- compare and order lengths, mass, volume/capacity and record the results using >, < and =
- recognise and use symbols for pounds (£) and pence (p); combine amounts to make a particular value
- find different combinations of coins that equal the same amounts of money
- solve simple problems in a practical context involving addition and subtraction of money of the same unit, including giving change
- compare and sequence intervals of time
- tell and write the time to five minutes, including quarter past/to the hour and draw the hands on a clock face to show these times
- know the number of minutes in an hour and the number of hours in a day.
|
|
Properties of Shape
|
Pupils should be taught to:
- recognise and name common 2-D and 3-D shapes, including:
- 2-D shapes [for example, rectangles (including squares), circles and triangles]
- 3-D shapes [for example, cuboids (including cubes), pyramids and spheres].
|
Pupils should be taught to:
- identify and describe the properties of 2-D shapes, including the number of sides and line symmetry in a vertical line
- identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces
- identify 2-D shapes on the surface of 3-D shapes, [for example, a circle on a cylinder and a triangle on a pyramid]
- compare and sort common 2-D and 3-D shapes and everyday objects.
|
|
Position and Direction
|
Pupils should be taught to:
- describe, position, direction and movement including whole, half, quarter and three quarter turns.
|
Pupils should be taught to:
- order and arrange combinations of mathematical objects in patterns and sequences
- use mathematical vocabulary to describe position, direction and movement, including movement in a straight line and distinguishing between rotation as a turn and in terms of right angles for quarter, half and three-quarter turns (clockwise and anticlockwise).
|
|
Statistics
|
|
Pupils should be taught to:
- interpret and construct simple pictograms, tally charts, block diagrams and simple tables
- ask and answer simple questions by counting the number of objects in each category and sorting the categories by quantity
- ask and answer questions about totalling and comparing categorical data.
|
Curriculum Content Coverage: Year 3 and 4
|
YEAR GROUP
|
Year 3
|
Year 4
|
|
Number and Place Value
|
- Pupils should be taught to:
- count from 0 in multiples of 4, 8, 50 and 100; find 10 or 100 more or less than a given number
- recognise the place value of each digit in a three-digit number (hundreds, tens, ones)
- compare and order numbers up to 1000
- identify, represent and estimate numbers using different representations
- read and write numbers up to 1000 in numerals and in words
- solve number problems and practical problems involving these ideas.
|
Pupils should be taught to
- count in multiples of 6, 7, 9, 25 and 1000
- find 1000 more or less than a given number
- count backwards through zero to include negative numbers
- recognise the place value of each digit in a four-digit number (thousands, hundreds, tens, and ones)
- order and compare numbers beyond 1000
- identify, represent and estimate numbers using different representations
- round any number to the nearest 10, 100 or 1000
- solve number and practical problems that involve all of the above and with increasingly large positive numbers
- read Roman numerals to 100 (I to C) and know that over time, the numeral system changed to include the concept of zero and place value.
|
|
Addition and Subtraction
|
Pupils should be taught to:
- add and subtract numbers mentally, including:
- a three-digit number and ones
- a three-digit number and tens
- a three-digit number and hundreds
- add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction
- estimate the answer to a calculation and use inverse operations to check answers
- solve problems, including missing number problems, using number facts, place value, and more complex addition and subtraction.
|
Pupils should be taught to:
- add and subtract numbers with up to 4 digits using the formal written methods of columnar addition and subtraction where appropriate
- estimate and use inverse operations to check answers to a calculation
- solve addition and subtraction two-step problems in contexts, deciding which operations and methods to use and why.
|
|
Multiplication and Division
|
Pupils should be taught to:
- recall and use multiplication and division facts for the 3, 4 and 8 multiplication tables
- write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for two-digit numbers times one-digit numbers, using mental and progressing to formal written methods
- solve problems, including missing number problems, involving multiplication and division, including positive integer scaling problems and correspondence problems in which n objects are connected to m objects.
|
Pupils should be taught to:
- recall multiplication and division facts for multiplication tables up to 12 × 12
- use place value, known and derived facts to multiply and divide mentally, including: multiplying by 0 and 1; dividing by 1; multiplying together three numbers
- recognise and use factor pairs and commutativity in mental calculations
- multiply two-digit and three-digit numbers by a one-digit number using formal written layout
- solve problems involving multiplying and adding, including using the distributive law to multiply two digit numbers by one digit, integer scaling problems and harder correspondence problems such as n objects are connected to m objects.
- Divide two digit and three digit numbers by a one digit number using the short division method- remainders within the answer but not in the final answer.
|
|
Fractions (including decimals and percentages)
|
Pupils should be taught to:
- count up and down in tenths; recognise that tenths arise from dividing an object into 10 equal parts and in dividing one-digit numbers or quantities by 10
- recognise, find and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators
- recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators
- recognise and show, using diagrams, equivalent fractions with small denominators
- add and subtract fractions with the same denominator within one whole [for example, 7/7 +1/7 = 6/7]
- compare and order unit fractions, and fractions with the same denominators
- solve problems that involve all of the above.
|
Pupils should be taught to:
- recognise and show, using diagrams, families of common equivalent fractions
- count up and down in hundredths; recognise that hundredths arise when dividing an object by one hundred and dividing tenths by ten.
- solve problems involving increasingly harder fractions to calculate quantities, and fractions to divide quantities, including non-unit fractions where the answer is a whole number
- add and subtract fractions with the same denominator
- recognise and write decimal equivalents of any number of tenths or hundredths
- recognise and write decimal equivalents to ¼, ½, ¾
- find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths
- round decimals with one decimal place to the nearest whole number
- compare numbers with the same number of decimal places up to two decimal places
- solve simple measure and money problems involving fractions and decimals to two decimal places.
-
|
|
Measurement
|
Pupils should be taught to:
- measure, compare, add and subtract: lengths (m/cm/mm); mass (kg/g); volume/capacity (l/ml)
- measure the perimeter of simple 2-D shapes
- add and subtract amounts of money to give change, using both £ and p in practical contexts
- tell and write the time from an analogue clock, including using Roman numerals from I to XII, and 12-hour and 24-hour clocks
- estimate and read time with increasing accuracy to the nearest minute; record and compare time in terms of seconds, minutes and hours; use vocabulary such as o’clock, a.m./p.m., morning, afternoon, noon and midnight
- know the number of seconds in a minute and the number of days in each month, year and leap year
- compare durations of events [for example to calculate the time taken by particular events or tasks].
|
Pupils should be taught to:
- Convert between different units of measure [for example, kilometre to metre; hour to minute]
- measure and calculate the perimeter of rectilinear figure (including squares) in centimetres and metres
- find the area of rectilinear shapes by counting squares
- estimate, compare and calculate different measures, including money in pounds and Pence
- read, write and convert time between analogue and digital 12- and 24-hour clocks
- solve problems involving converting from hours to minutes; minutes to seconds; years to months; weeks to days.
|
|
Properties of Shape
|
Pupils should be taught to:
- draw 2-D shapes and make 3-D shapes using modelling materials; recognise 3-D shapes in different orientations and describe them
- recognise angles as a property of shape or a description of a turn
- identify right angles, recognise that two right angles make a half-turn, three make three quarters of a turn and four a complete turn; identify whether angles are greater than or less than a right angle
- identify horizontal and vertical lines and pairs of perpendicular and parallel lines.
|
Pupils should be taught to:
- compare and classify geometric shapes, including quadrilaterals and triangles, based on their properties and sizes
- identify acute and obtuse angles and compare and order angles up to two right angles by size
- identify lines of symmetry in 2-D shapes presented in different orientations
- complete a simple symmetric figure with respect to a specific line of symmetry.
|
|
Position and Direction
|
-
|
Pupils should be taught to:
- describe positions on a 2-D grid as coordinates in the first quadrant
- describe movements between positions as translations of a given unit to the left/right
- and up/down
- plot specified points and draw sides to complete a given polygon.
|
|
Statistics
|
Pupils should be taught to:
- interpret and present data using bar charts, pictograms and tables
- solve one-step and two-step questions [for example, ‘How many more?’ and ‘How many fewer?’] using information presented in scaled bar charts and pictograms and tables.
|
Pupils should be taught to:
- interpret and present discrete and continuous data using appropriate graphical methods, including bar charts and time graphs.
- solve comparison, sum and difference problems using information presented in bar charts, pictograms, tables and other graphs.
|
Curriculum Content Coverage: Year 5 and 6
|
YEAR GROUP
|
Year 5
|
Year 6
|
|
Number and Place Value
|
Pupils should be taught to:
- read, write, order and compare numbers to at least 1 000 000 and determine the value of each digit
- count forwards or backwards in steps of powers of 10 for any given number up to 1 000 000
- interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers, including through zero
- round any number up to 1 000 000 to the nearest 10, 100, 1000, 10 000 and 100 000
- solve number problems and practical problems that involve all of the above
- read Roman numerals to 1000 (M) and recognise years written in Roman numerals.
|
Pupils should be taught to:
- read, write, order and compare numbers up to 10 000 000 and determine the value of each digit
- round any whole number to a required degree of accuracy
- use negative numbers in context, and calculate intervals across zero
- solve number and practical problems that involve all of the above.
|
|
Addition and Subtraction
|
Pupils should be taught to:
- add and subtract whole numbers with more than 4 digits, including using formal written methods (columnar addition and subtraction)
- add and subtract numbers mentally with increasingly large numbers
- use rounding to check answers to calculations and determine, in the context of a problem, levels of accuracy
- solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why.
|
Pupils should be taught to:
- multiply multi-digit numbers up to 4 digits by a two-digit whole number using the formal written method of long multiplication
- divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context
- divide numbers up to 4 digits by a two-digit number using the formal written method of short division where appropriate, interpreting remainders according to the context
- perform mental calculations, including with mixed operations and large numbers
- identify common factors, common multiples and prime numbers
- use their knowledge of the order of operations to carry out calculations involving the four operations
- solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why
|
|
Multiplication and Division
|
Pupils should be taught to:
- identify multiples and factors, including finding all factor pairs of a number, and common factors of two numbers
- Know and use the vocabulary of prime numbers, prime factors and composite (non-prime) numbers
- establish whether a number up to 100 is prime and recall prime numbers up to 19
- multiply numbers up to 4 digits by a one- or two-digit number using a formal written method, including long multiplication for two-digit numbers
- multiply and divide numbers mentally drawing upon known facts
- divide numbers up to 4 digits by a one-digit number using the formal written method of short division and interpret remainders appropriately for the context
- multiply and divide whole numbers and those involving decimals by 10, 100 and 1000
- recognise and use square numbers and cube numbers, and the notation for squared (2) and cubed (3)
- solve problems involving multiplication and division including using their knowledge of factors and multiples, squares and cubes
- solve problems involving addition, subtraction, multiplication and division and a combination of these, including understanding the meaning of the equals sign
- solve problems involving multiplication and division, including scaling by simple fractions and problems involving simple rates.
- Solve problems involving multiplication and division where larger numbers are used by decomposing them into their factors.
|
|
Fractions (including decimals and percentages)
|
Pupils should be taught to:
- compare and order fractions whose denominators are all multiples of the same number
- identify, name and write equivalent fractions of a given fraction, represented visually, including tenths and hundredths
- recognise mixed numbers and improper fractions and convert from one form to the other and write mathematical statements > 1 as a mixed number [for example, 2/5 + 4/5 = 6/5 = 1 1/5 ]
- add and subtract fractions with the same denominator and denominators that are multiples of the same number
- multiply proper fractions and mixed numbers by whole numbers, supported by materials and diagrams
- read and write decimal numbers as fractions [for example, 0.71 = 71/100 ]
- recognise and use thousandths and relate them to tenths, hundredths and decimal equivalents
- round decimals with two decimal places to the nearest whole number and to one decimal place
- read, write, order and compare numbers with up to three decimal places
- solve problems involving number up to three decimal places
- recognise the per cent symbol (%) and understand that per cent relates to ‘number of parts per hundred’, and write percentages as a fraction with denominator 100, and as a decimal
- solve problems which require knowing percentage and decimal equivalents of ½ , ¼, 1/5, 2/5, 4/5and those fractions with a denominator of a multiple of 10 or 25.
|
Pupils should be taught to:
- use common factors to simplify fractions; use common multiples to express fractions in the same denomination
- compare and order fractions, including fractions > 1
- add and subtract fractions with different denominators and mixed numbers, using the concept of equivalent fractions
- multiply simple pairs of proper fractions, writing the answer in its simplest form [for example, ¼ x ½ = 1/8
- divide proper fractions by whole numbers [for example, 1/3 ÷ 2 = 1/6]
- associate a fraction with division and calculate decimal fraction equivalents [for example, 0.375] for a simple fraction [for example, 3/8]
- identify the value of each digit in numbers given to three decimal places and multiply and divide numbers by 10, 100 and 1000 giving answers up to three decimal places
- multiply one-digit numbers with up to two decimal places by whole numbers
- use written division methods in cases where the answer has up to two decimal places
- solve problems which require answers to be rounded to specified degrees of accuracy
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
|
|
Measurement
|
Pupils should be taught to:
- convert between different units of metric measure (for example, kilometre and metre; centimetre and metre; centimetre and millimetre; gram and kilogram; litre and millilitre)
- understand and use approximate equivalences between metric units and common imperial units such as inches, pounds and pints
- measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres
- calculate and compare the area of rectangles (including squares), and including using standard units, square centimetres (cm2) and square metres (m2) and estimate the area of irregular shapes
- estimate volume [for example, using 1 cm3blocks to build cuboids (including cubes)] and capacity [for example, using water]
- solve problems involving converting between units of time
- use all four operations to solve problems involving measure [for example, length, mass, volume, money] using decimal notation, including scaling.
|
Pupils should be taught to:
- solve problems involving the calculation and conversion of units of measure, using decimal notation up to three decimal places where appropriate
- use, read, write and convert between standard units, converting measurements of length, mass, volume and time from a smaller unit of measure to a larger unit, and vice versa, using decimal notation to up to three decimal places
- convert between miles and kilometres
- recognise that shapes with the same areas can have different perimeters and vice versa
- recognise when it is possible to use formulae for area and volume of shapes
- calculate the area of parallelograms and triangles
- calculate, estimate and compare volume of cubes and cuboids using standard units, including cubic centimetres (cm3) and cubic metres (m3), and extending to other units [for example, mm3 and km3].
|
|
Properties of Shape
|
Pupils should be taught to:
- identify 3-D shapes, including cubes and other cuboids, from 2-D representations
- know angles are measured in degrees: estimate and compare acute, obtuse and reflex angles
- draw given angles, and measure them in degrees (o)
- identify:
- angles at a point and one whole turn (total 360o)
- angles at a point on a straight line and 1/2 a turn (total 180o)
- other multiples of 90o
- use the properties of rectangles to deduce related facts and find missing lengths and angles
- distinguish between regular and irregular polygons based on reasoning about equal sides and angles.
|
Pupils should be taught to:
- draw 2-D shapes using given dimensions and angles
- recognise, describe and build simple 3-D shapes, including making nets
- compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons
- illustrate and name parts of circles, including radius, diameter and circumference and know that the diameter is twice the radius
- recognise angles where they meet at a point, are on a straight line, or are vertically opposite, and find missing angles.
|
|
Position and Direction
|
Pupils should be taught to:
- identify, describe and represent the position of a shape following a reflection or translation, using the appropriate language, and know that the shape has not changed.
|
Pupils should be taught to:
- describe positions on the full coordinate grid (all four quadrants)
- draw and translate simple shapes on the coordinate plane, and reflect them in the axes.
|
|
Statistics
|
Pupils should be taught to:
- solve comparison, sum and difference problems using information presented in a line graph
- complete, read and interpret information in tables, including timetables.
|
Pupils should be taught to:
- interpret and construct pie charts and line graphs and use these to solve problems
- calculate and interpret the mean as an average.
|
|
Ratio and Proportion
|
-
|
Pupils should be taught to:
- solve problems involving the relative sizes of two quantities where missing values can be found by using integer multiplication and division facts
- solve problems involving the calculation of percentages [for example, of measures, and such as 15% of 360] and the use of percentages for comparison
- solve problems involving similar shapes where the scale factor is known or can be found
- solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
|
|
Algebra
|
-
|
Pupils should be taught to:
- use simple formulae
- generate and describe linear number sequences
- express missing number problems algebraically
- find pairs of numbers that satisfy an equation with two unknowns
- enumerate possibilities of combinations of two variables.
|
Strategies/Skills/Key subject disciplines
Alongside the above content, at Westgate Academy, we use other strategies to support children’s mathematical understanding. White Rose Maths documents are used as a resource to support the planning and teaching of Maths at Westgate Academy.
Other strategies used include:
RUCSAC

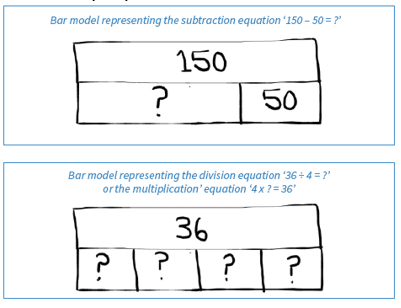
Bar Model
Part/Whole Bar Model:
Part/whole bar models are made up of parts and wholes, where the whole represents the sum of the parts. This type of bar model is frequently used to represent; all four operations (including calculations involving more than one pair of numbers), fractions, measure, algebra, ratio and proportion and much more.
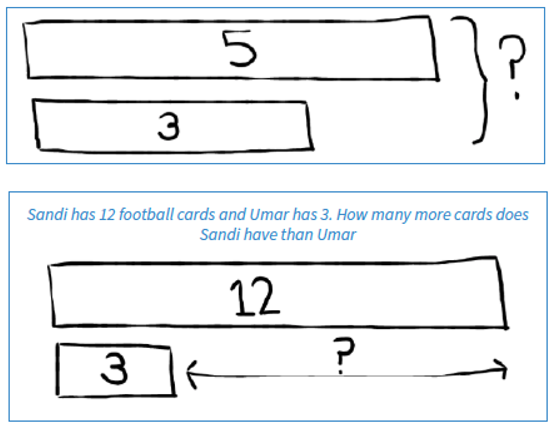
Comparison Bar Model:
Rather than having a bar which represents the ‘whole’ in a problem, in a comparison bar model two or more vertically aligned bars are drawn to help children to compare two (or more) amounts.
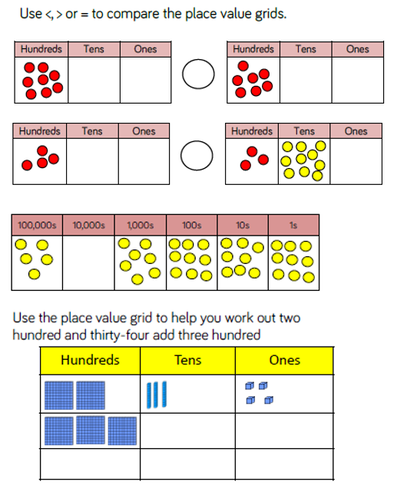
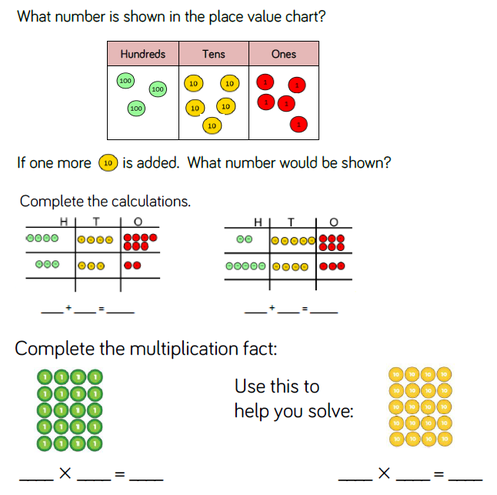
Place Value Charts
Place value charts are useful when teaching place value, addition, subtraction, multiplication and division.
Place Value Counters
Place value counters are useful when teaching place value, addition, subtraction, multiplication and division.
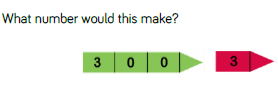
Arrow Cards
Arrow cards are useful when teaching place value.
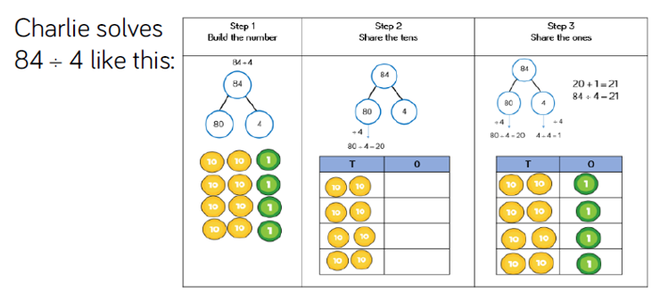
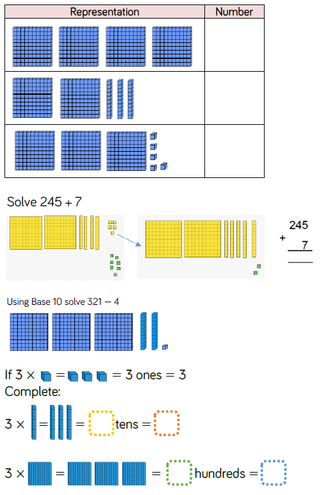
Base Ten Equipment
Base Ten equipment are useful when teaching place value, addition, subtraction, multiplication and division.
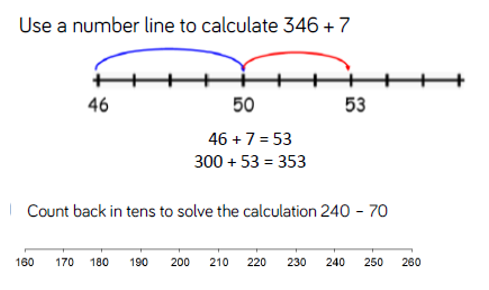
Number Lines
Number lines are useful when teaching place value, addition, subtraction and multiplication (as repeated addition).
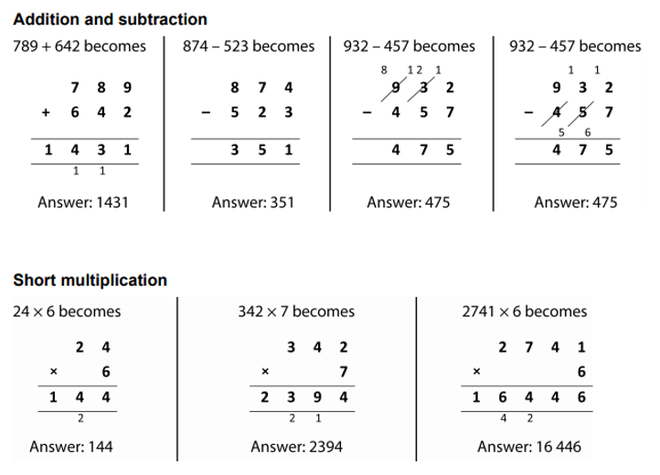
Formal Written Method Strategies

Vocabulary
ALL OF KEY STAGE 2 AND YEAR 3
|
Number and Place Value
|
Addition and Subtraction
|
Multiplication and Division
|
Measure
|
- Number
- Zero, one, two, three… twenty, one hundred, one thousand and beyond
- None
- Count (on/up/to/from/down)
- Before, after
- More, less, many, few, fewer, least, fewest, smallest, greater, lesser
- Equal to, the same as
- Odd, even
- Pair
- Units, ones, tens
- Ten more/less
- Digit
- Numeral
- Figure(s)
- Compare
- (In) order/a different order
- Size
- Value
- Between, halfway between
- Above, below
- Numbers to one hundred
- Hundreds
- Partition, recombine
- Place, place value
- Hundred more/less
- Numbers to one thousand
- One/two/three-digit number
- Sequence, pattern, rule, relationship
|
- Number bonds, number line
- Add, more, plus, make, sum, total, altogether
- Inverse
- Double, near double
- Half, halve
- Equals, is the same as (including equals sign)
- Difference between
- How many more to make..?, how many more is…than..?, how much more is..?
- Subtract, take away, minus
- How many fewer is…than..?, how much less is..?
- Column addition and subtraction
- How many are left/left over?
- Tens boundary, hundreds boundary
|
- Odd, even
- Count in twos, threes, fives
- Count in tens (forwards from/backwards from)
- How many times?
- Lots of, groups of
- Once, twice, three times, five times
- Multiple of, times, multiply, multiply by, multiple of
- Repeated addition
- Array, row, column
- Double, halve
- Share, share equally
- Group in pairs, threes, etc.
- Equal groups of
- Divide, divided by, left, left over
- Product
- Multiples of four, eight, fifty and one hundred
- Scale up
- Remainder
|
- Full, half full, empty
- Holds, container
- Weigh, weighs, balances
- Heavy, heavier, heaviest, light, lighter, lightest
- Scales
- Time
- Days of the week: Monday, Tuesday, etc.
- Months of the year January, February etc.
- Seasons: spring, summer, autumn, winter
- Day, week, month, year, weekend
- Birthday, holiday, century
- Calendar, Date
- Morning, afternoon, evening, night, midnight
- Bedtime, dinnertime, playtime
- Today, yesterday, tomorrow
- Before, after, next, last, now, soon, early, late
- Quick, quicker, quickest, quickly , fast, faster, fastest, slow, slower, slowest, slowly
- Old, older, oldest, new, newer, newest
- Takes longer, takes less time
- Hour, o'clock, half past, clock, watch, hands
- How long ago?, how long will it be to…?, how long will it take to…?, how often?
- Once, twice, first, second, third, etc.
- Estimate, close to, about the same as, just over, just under
- Too many, too few, not enough, enough
- Length, width, height, depth
- Long, longer, longest, short, shorter shortest, tall, taller, tallest, high, higher, highest
- Low, wide, narrow, deep, shallow, thick, thin
- Far, near, close
- Metre, ruler, metre stick
- Money, coin, penny, pence, pound, note price, cost, buy, sell, spend, spent, pay, change, dear(er), costs more, costs less, cheaper, costs the same as
- How much?, how many?, total
- Bought, Sold
- Most expensive/more expensive
- Least expensive/less expensive
- Amount, Value, Worth
- Quarter past/to
- Centimetre (cm), Millimetre (mm), Metre (m)
- Kilometre (km), Mile
- Measure
- Compare
- Measuring scale
- Estimate, approximate, approximately
- Balance
- Weight
- Temperature (degrees)
- Leap year
- Twelve-hour/twenty-four- hour clock
- Am/pm
- Timetable
- Arrival/departure
- Minute, Second
- Digital/analogue clock/watch/timer
- Roman numerals I to XIII
|
|
Geometry (properties of shapes)
|
Geometry (position and direction)
|
Fractions
|
Data/Statistics
|
Algebra
|
|
- Group, sort
- Cube, cuboid, pyramid, sphere, cone, cylinder, circle, triangle, square
- Circular, semi-circle
- Triangular
- Rectangle, rectangular
- Pentagon, pentagonal
- Hexagon, hexagonal
- Octagon, octagonal
- Quadrilateral
- Surface
- Vertex, vertices
- Prism
- Shape
- Flat, curved, straight, round
- Hollow, solid
- Corner (point, pointed)
- Face, side, edge
- Make, build, draw
- Size
- Bigger, larger, smaller
- Symmetrical, line of symmetry
- Fold
- Match
- Mirror line, reflection
- Pattern, repeating pattern
- Horizontal, perpendicular and parallel lines
- 3D, three dimensional
- 2D, two dimensional
|
- Position
- Over, under, underneath, above, below, top, bottom, side
- on, in, outside, inside
- around, in front, behind
- Front, back
- Before, after
- Beside, next to, Opposite
- Apart
- Between, middle, edge, centre
- Corner
- Direction
- Journey
- Left, right, up, down, forwards, backwards, sideways
- Across
- Close, far, near
- Along, through
- To, from, towards, away from
- Movement
- Slide, roll, turn, whole turn, half turn
- Stretch, bend
- Clockwise, anticlockwise
- Straight line
- Ninety degree turn, right angle
- Greater/less than ninety degrees
- Orientation (same orientation, different orientation)
- Protractor
- Ascend/descend
- Quarter turn
- Grid
- Row, column
- North, South, East, West
- Horizontal, vertical, diagonal
|
- Whole
- Fraction
- Part
- Equal parts, four equal parts
- One half, two halves
- One quarter, two quarters
- Three quarters, one third, a third
- Equivalence, equivalent
- Numerator, denominator
- Unit fraction, non-unit fraction
- Compare and order
- Tenths
|
- Count, tally, tally chart, sort
- Vote
- Graph, block graph, pictogram,
- Represent
- Group, set, list, table
- Label, title
- Most popular, most common, least popular, least common
- Chart, bar chart, frequency table, Carroll diagram, Venn diagram
- Axis, axes
- Diagram
|
|
|
|
General/Problem Solving
|
- Listen, join in
- Say, think, imagine, remember
- Start from, start with, start at
- Look at, point to
- Put, place, fit
- Arrange, rearrange
- Change, change over
- Split, separate
- Carry on, continue, repeat, what comes next?
- Find, choose, collect, use, make, build
- Tell me, describe, pick out, talk about, explain, show me
- Read, write, record, trace, copy, complete, finish, end
- Fill in, shade, colour, tick, cross, draw, draw a line between, join (up), ring, arrow
- Cost
- Count, work out, answer, check same number(s)/different number(s)/missing number(s)
- Number facts, number line, number track, number square, number cards
- Abacus, counters, cubes, blocks, rods, die, dice, dominoes, pegs, peg board
- Same way, different way, best way, another way
- In order, in a different order
- Not all, every, each
- Predict
- Describe the pattern, describe the rule
- Find, find all, find different
- Investigate
- Calculate
- Mental Calculation
- Method
|
Year 4
|
Number and Place Value
|
Addition and Subtraction
|
Multiplication and Division
|
Measure
|
|
PLEASE SEE THE KEY STAGE 2/YEAR 3 VOCABULARY LIST
|
- Tenths, hundredths
- Thousands, ten thousand, hundred thousand, million.
- Four-digit number
- Decimal (places)
- Round up/down, nearest, to nearest one/ten, hundred etc.
- Thousand more/less than
- Negative integers
- Count through zero
- Roman numerals (I to C)
- < >
- Integer
- Above/below zero, minus
- Positive, negative.
- Next, consecutive
- Sort, classify, property
|
|
- Multiplication facts (up to 12x12)
- Division facts
- Inverse
- Derive
- Divisible by
- Inverse
- Factor
- Quotient
|
- Measurement
- Unit, standard unit, metric unit, imperial unit.
- Breadth
- Convert
- Perimeter
- Edge
- Area, covers
- Square centimetre (cm²)
- Measuring cylinder
- Millennium
- Date of birth
- Noon
|
|
Geometry (properties of shapes)
|
Geometry (position and direction)
|
Fractions
|
Data/Statistics
|
Algebra
|
- Perimeter and area
- Quadrilaterals
- Angle, line
- Right angle, acute and obtuse angles
- Radius, diameter
- Construct, net
- Square-based
- Triangular-based
- Tetrahedron
- Polyhedron
- Equilateral triangle, isosceles triangle, scalene triangle
- Trapezium, Parallelogram, Rhombus, Kite
- Oblong
- Heptagon
- Polygon
- Spherical, cylindrical
- Line symmetry
- Reflect
- Regular and irregular polygons
|
- Rotate, rotation
- Degree
- Origin
- Coordinates
- Translation
- Quadrant
- x-axis, y-axis
- Angle measurer, compass
- North-east (NE), north-west (NW), south-east (SE), south-west (SW)
- Plot
|
- Eighth, sixth, fifth, tenth, twentieth
- Proportion
- In every, for every
- Decimal
- Decimal point
- Decimal place
- Equivalent decimals
- Equivalent fractions
|
- Continuous data
- Line graph
- Tally chart
- Survey, questionnaire, data
|
|
Year 5
|
Number and Place Value
|
Addition and Subtraction
|
Multiplication and Division
|
Measure
|
|
PLEASE SEE THE KEY STAGE 2/YEAR 3 AND YEAR 4 VOCABULARY LIST
|
- Powers of 10
- ≤ greater than or equal to
- ≥ less than or equal to
- Ascending/descending order
- Round to the nearest thousand
- Approximately equivalent to
- Formula
|
- Efficient written method
- Ones boundary, tenths boundary.
|
- Factor pairs
- Composite numbers, prime number, prime factors, square number, cubed number
- Formal written method
- Divisibility
|
- Volume
- Imperial units, metric units
- Inches, feet, yards, mile
- Pounds, ounces, stone, tonne
- Pints, gallons
- Square metre (m²)
- Discount
- Currency
|
|
Geometry (properties of shapes)
|
Geometry (position and direction)
|
Fractions
|
Data/Statistics
|
Algebra
|
- Regular and irregular polygons
- Acute, obtuse
- Octahedron
- Reflective symmetry
- Reflex angle
- Protractor
- Parallel
- Perpendicular
|
- Dimensions
- Quadrant
- X-axis, y-axis
|
- Proper fractions, improper fractions, mixed numbers
- Reduce to, cancel
- Percentage
- Half, quarter, fifth, two fifths, four, fifths, ninth, twelfth, hundredth
- Ratio, proportion
- Ratio
- Proper/improper fraction
- Per cent %
|
- Database
- Line graph
- Maximum and minimum value
|
- Linear number sequence
- Substitute
- Variables
- Symbol
- Known values
|
Year 6
|
Number and Place Value
|
Addition and Subtraction
|
Multiplication and Division
|
Measure
|
|
PLEASE SEE THE KEY STAGE 2/YEAR 3, YEAR 4 AND YEAR 5 VOCABULARY LIST
|
|
|
|
- Order of operations
- Common factors, common multiples
- Factorise
|
- Profit
- Loss
- Circumference
- Yard, feet. Foot, inches, inch
- Tonne
- Pound (lb), ounce (oz)
- Centilitre (cl)
- Greenwich Mean Time, British Summer Time.
|
|
Geometry (properties of shapes)
|
Geometry (position and direction)
|
Fractions
|
Data/Statistics
|
Algebra
|
- Vertically opposite (angles)
- Circumference, radius, diameter
- Dodecahedron
- Intersect/intersection
- Rhombus
- Parallelogram, Trapezium
|
- Four quadrants (for coordinates)
|
- Degree of accuracy
- Simplify
- Thousandth
|
- Mean
- Pie chart
- Construct
- Average
- Statistics
|
- Linear number sequence
- Substitute
- Variables
- Symbol
- Known values
|
Implementation
At Westgate Academy, children will take part in a discrete Maths lesson for at least an hour each day. In Year 3, 4 and 5, planning and teaching follows the White Rose Maths schemes of learning.
In Year 6, planning and teaching is structured differently in preparation for the end of KS2 SATs. Until February, the objectives from the following blocks are taught: place value; addition and subtraction; multiplication and division; fractions, decimals and percentages; algebra; ratio and proportion; and measures. From February onwards, Year 6 teach and plan according to our in-house revision scheme- SATs ATTACK. This is a scheme which aims to cover/revise all Year 6 Maths objectives in preparation for the end of KS2 SATs. Children are provided with weekly pre-learning and home learning based on the weekly/fortnightly Maths focus.
In addition, children will also have an opportunity to take part in a short fluency/arithmetic three times a week. This in a chance for children to practise arithmetic/fluency skills that they have already been taught; therefore, revisiting and embedding fundamental Maths skills.
Daily, fluid Maths intervention also takes place in each class. This is an extra, small-group intervention for: children who may have struggled with the previous day’s learning; children who may need a little more practise to boost their confidence; or children who may need or want an extra challenge. If a child is absent (for a short period of time) and the learning from that day is a new concept, these children will then attend an intervention group to catch up with the missed learning- if required.
During Maths lessons across the school, differentiation can be clearly seen. In Year 3, 4 and 5, the concept of Bronze, Silver, Gold and Platinum/Cheeky Challenge are used- with Bronze being the easiest or more scaffolded level of learning, and Gold and Platinum being the most challenging or problem solving-based learning. In Year 6, the concept of Tricky, Trickier, Trickiest and Cheeky Challenge are used- with Tricky being the easiest or more scaffolded level of learning, and Trickiest and Cheeky Challenge being the most challenging or problem solving-based learning. Children are asked or choose to start at a particular level of learning- dependent on their ability or need. This is a flexible approach, and children may start on different levels depending on their understanding and confidence. Most Maths lessons (depending on the type of activity), allow children to move through the different levels of learning.
Fluency, Reasoning and Problem Solving are areas that you will see in both lessons and books. At Westgate Academy, we feel that it is essential that pupils have a solid grasp with Fluency as this underpins all of their Maths understanding. In specific Fluency lessons, before children move their Maths on to the next level, they have to prove their understanding by completing a Reasoning Task. This system is not applicable in lessons where the activities are reasoning and problem solving based. At Westgate Academy, we believe that for a true depth of understanding, children need to be able to reason and problem solve at their own level. Therefore, this can be seen through our use of Reasoning Tasks and reasoning and problem solving-based lessons.
At the beginning of every lesson, children complete any corrections from the previous lesson. Once these are complete, children then take part in the Flashback Task. This is a White Rose Maths Flashback 4 task. This is another opportunity for children to embed what they have previously learnt (spaced learning).
Throughout the Maths lessons at Westgate Academy, we are developing opportunities to highlight Maths connections. We have introduced the ‘Maths Connector’ clipart which can be displayed on slides. This prompts the children to answer the question: What is the Maths link? Also throughout lessons, children are given the opportunities to take part in mathematical talk through ‘Let’s Talk Maths’. This offers children to discuss mathematical concepts with a focus on particular vocabulary.
Maths lessons at Westgate Academy aim to support all learners’ needs. Alongside our differentiation, we support our SEN learners with adult support, hands on resources and learning that meets their needs. For the More Able children in some classes (where applicable), children may start their learning earlier compared to other pupils- to reduce their ‘listening time’ when they already feel confident. In some classes, the More Able pupils may be asked to ‘Grapple’ with their maths learning before working with the class teacher. In addition to this, some of these children may have access to a pre-learning group or an intervention group for extra challenge.
In some year groups, children are provided with times tables to learn each week- as part of their home learning. Children are then asked to complete a weekly times tables test.
In Maths, all learning is marked with an S for success (and a D for development where applicable). Any corrections are marked with a C and children complete these at the start of their next lesson.
Staff CPD
Staff have taken part in various CPD sessions and have worked hard to implement new initiatives. Training has included:
- Introduction of Daily Fluency.
- Learning walls.
- Instant feedback during lessons.
- Bar modelling strategy.
- Integrating reasoning and problem solving into everyday lessons.
- Maths work moderation across year groups.
- Maths connections.
- Types of learning- surface, silo and interconnected learning.
- WRM- CPA and Bar Modelling.
Maths Leader CPD
- NCETM Accredited PD Lead.
- SLE for Kyra Teaching Alliance.
- Attended Kyra SLE workshops based on Effective CPD and Research Schools.
- Attended Maths Hub meetings.
- Attended Kyra Maths Leader forums.
- Attended the NCETM Mastery Maths training- specialising in supporting mixed aged classes.
- Attended the LENS project leader training.
- Led staff training at other schools- focusing on reasoning and problem solving.
- Led the QFT training for the LENS project.
- Completed school visits as part of the LENS project.
Opportunities to revisit learning
Due to the nature of the National Curriculum for Mathematics, children are able to revisit mathematical concepts again each year. These concepts and skills are built upon as children progress through the school.
As certain maths concepts are taught in ‘blocks’ (in line with the White Rose Maths scheme), it is important that teachers make clear links back to previous learning/maths concepts wherever possible. For example, when teaching area teachers need to make clear, explicit links back to multiplication, times tables, properties of 2D shapes etc.
As part of our topic lessons, maths links are made wherever possible.
|
Year Group
|
TOPIC
|
Maths Links
|
|
Year 3
|
PAST
|
Ordering key events in history and the Roman era.
|
|
PRESENT
|
Map work- identifying local places (coordinates)
|
|
Map work- identifying countries in Great Britain (four figure grid references and 8 points of a compass)
|
|
Map work- name and locate cities in Britain (four figure grid references and 8 points of a compass)
|
|
Year 4
|
PAST
|
Ordering key events in history and the Tudor era.
|
|
PRESENT
|
Map work- name and locate countries in Europe (four figure grid references and 8 points of a compass)
|
|
Field work activity- statistics. Interpret and present discrete and continuous data.
|
|
Field work activity- statistics. Solve comparison, sum and difference problems using bar charts.
|
|
PICK
|
Classification keys.
|
|
Year 5
|
PAST
|
Ordering key events in history and the Victorian era.
|
|
Statistics. Analysing data based on trade goods imported into the UK during the Victorian era.
|
|
PRESENT
|
Map work- name and locate major physical features of the Americas (four figure grid references and 8 points of a compass)
|
|
Map work- name and locate major cities in the Americas (four figure grid references and 8 points of a compass)
|
|
Statistics. Analysing earthquake data. Population data and the impact of earthquakes on this.
|
|
Year 6
|
PAST
|
Ordering key events in history.
|
|
Ordering key events during WW1.
|
|
Ordering key events during WW2.
|
|
Rationing activity. Links to four operations.
|
|
PRESENT
|
Map work- name and locate major countries in the world (four figure grid references and 8 points of a compass). Also focus on longitude, latitude, hemispheres and tropics.
|
|
Deforestation: use of statistics.
|
|
Population growth. Analysing statistics
|
In other areas of the curriculum, maths links are also made wherever possible.
|
Science
|
- Statistics
- Measures
- Geometry
- Number
|
|
Art
|
- Symmetrical art can be analysed and the number of lines of symmetry can be found. Also, the order of rotational symmetry can be studied.
- Ratio is used to mix paints. For example, to make purple, you mix 3 parts red to 7 parts blue.
- Perspective can be used to show enlargement of shapes on square paper in KS2 maths.
|
|
Design and Technology
|
- Reading Scales.
- Measuring ingredients and working out proportions.
- Using ratios in recipes.
- Being able to measure things accurately is an important skill in both D&T and mathematics.
- Estimation is also important when working out quantities of raw materials.
|
|
Computing
|
- Information can be represented in Excel and calculations using formula can be done on the data here too.
- Scratch Maths allows children to use their mathematical skills to program computers.
|
|
Languages
|
- Numbers can be used to do calculations or times tables
|
SMSC and British Values
Children will have opportunities to:
SMSC
Spiritual Education
Use imagination and creativity to explore ideas while learning mathematics by: identifying and applying patterns and rules to everyday problem-solving; writing own problems and challenges that use those patterns or rules.
Moral Education
Understanding the consequences of actions: Eg. If you perform a particular action to one number, will the same outcome apply to other numbers? Is it always the case? ‘Sometimes, always, never’ statements.
Social Education
Developing personal qualities and using social skills: Working in pairs or groups to solve problems; Perseverance when struggling to answer questions; not being afraid to try – it’s ok to be wrong, it’s not ok not to try; taking turns when playing maths games. Participating, co-operating and resolving conflicts: as above, but also ‘X thinks ___, Y thinks ___, who is right?’ type questions.
Cultural Education
Understanding and appreciating personal influences: taking into account other people’s views and understanding how to express own views. Eg. How to explain to someone where they may have gone wrong in a question.
BRITISH VALUES
Democracy
Take into account the views of others in shared activities. Voting when collecting data.
The Rule of Law
Undertake safe practices, following class rules during tasks and activities for the benefit of all. Understand the consequences if rules are not followed.
Individual Liberty
Work within boundaries to make safe choices during practical activities. Make own choices within data handling activities.
Tolerance of those with different faiths and beliefs
Use maths to learn about different faiths and cultures around the world. Eg. looking at patterns/shapes within Islam / Hindu religions.
Mutual Respect
To behave appropriately, allowing all participants the opportunity to work effectively. Take turns and share equipment. Review each other’s work respectfully. Work collaboratively on projects/problems, help and advise others.
Impact
How will Maths be assessed at Westgate Academy?
Teacher assessment takes place through daily marking and feedback.
Daily intervention takes place. Children’s confidence/understanding is RAG rated at the end of each session.
Across the school, class teachers are using the White Rose Maths unit assessments to track children’s mathematical understanding. These are to be used after the next unit of learning (e.g. the place value assessment to be conducted after the addition and subtraction unit- links with spaces learning). Class teachers to then plan in opportunities for weaknesses to be addressed.
In addition, Maths is assessed at each Assessment Point:
Formal Assessment Procedures:
At Westgate Academy, we have three assessment points each academic year.
September: Year 3 and Year 6 complete a Baseline assessment.
December: Assessment Point 1 (AP1).
March: Assessment Point 2 (AP2).
May: KS2 SATs assessments.
June: Assessment Point 3 (AP3).
In year 3, 4 and 5 (for children working at Y1, 3, 4 and 5 expectations), children are assessed using the NfER assessment papers. From these, scaled scores are tracked using our Westgate Tracking system.
In year 3, 4 and 5 (for children working at Y2 expectations), children are assessed using the KS1 SATs assessments. From these, scaled scores are tracked using our Westgate Tracking system.
In year 6, most children are assessed using previous KS2 SATs assessments. From these, scaled scores are tracked using our Westgate Tracking system. Children working significantly below ARE will be assessed by the NfER assessment papers.
Pupils’ strengths and weaknesses (for each assessment point) are then recorded and are addressed in the following lessons. These are also sent to the Maths subject lead.
At the End of Key Stage 2, Year 6 children complete the end of KS2 assessments, which includes one Arithmetic paper and two Reasoning papers.
How will the impact of our Maths curriculum be evaluated/monitored?
The Maths subject leader is responsible for the monitoring and evaluation of this subject area. Monitoring is scheduled to occur half-termly. Judgements on the impact of the curriculum on pupils is based upon a triangulation of different monitoring and evaluation activities within school:
- Lesson observations
- Learning walks
- Pupil voice discussions
- Book and planning scrutinies
- Outcomes of assessments
- Deep dives












